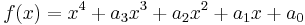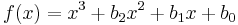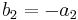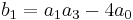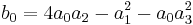Resolvent cubic

In mathematics, a resolvent cubic polynomial is defined as follows:

Let

$f(x)=x^4%2Ba_3x^3%2Ba_2x^2%2Ba_1x%2Ba_0 \,$

be a monic quartic polynomial. The resolvent cubic is the monic cubic polynomial

$f(x)= x^3%2Bb_2x^2%2Bb_1x%2Bb_0 \,$

where

$b_2 = -a_2 \,$

$b_1 = a_1a_3 - 4a_0 \,$

$b_0 = 4a_0a_2 - a_1^2 -a_0a_3^2 \,$

This can be used to solve the roots of the quartic by solving for the roots of a cubic.

External references